


suivant: 3D-VAR incrémental
monter: Assimilation variationnelle
précédent: Assimilation variationnelle
Table des matières
Nous notons encore 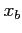 l'ébauche de la condition initiale,
l'ébauche de la condition initiale, 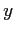 le
vecteur des observations du système,
le
vecteur des observations du système, 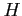 l'opérateur
d'observations permettant de relier un état
l'opérateur
d'observations permettant de relier un état 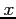 du système aux
observations
du système aux
observations 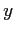 . La méthode du 3D-VAR (méthode variationnelle
à 3 dimensions) consiste à minimiser une fonction coût qui
mesure à la fois l'erreur sur la condition initiale et l'erreur sur
les observations :
. La méthode du 3D-VAR (méthode variationnelle
à 3 dimensions) consiste à minimiser une fonction coût qui
mesure à la fois l'erreur sur la condition initiale et l'erreur sur
les observations :
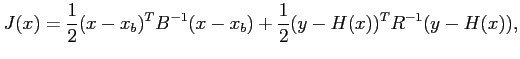 |
(2.14) |
où 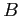 et
et 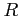 sont les matrices de covariance d'erreur sur
respectivement la condition initiale et les observations. La
minimisation s'effectue en général avec un algorithme de type BFGS
(voir le chapitre suivant) qui ne nécessite que la connaissance du
gradient de la fonction coût pour la minimiser. En supposant que
sont les matrices de covariance d'erreur sur
respectivement la condition initiale et les observations. La
minimisation s'effectue en général avec un algorithme de type BFGS
(voir le chapitre suivant) qui ne nécessite que la connaissance du
gradient de la fonction coût pour la minimiser. En supposant que 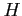 est linéaire, celui-ci est évidemment :
est linéaire, celui-ci est évidemment :
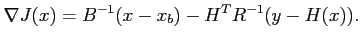 |
(2.15) |
Lorsque des algorithmes de type Newton sont utilisés (uniquement lorsque
la dimension du problème le permet), il faut également connaître
le hessien de la fonction coût
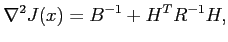 |
(2.16) |
indépendant de 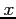 (toujours dans l'hypothèse où
(toujours dans l'hypothèse où 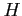 est linéaire).
est linéaire).
Le point de départ de la minimisation est souvent une ébauche de
la condition initiale, résultat d'une prévision passée. Lorsque
la minimisation aboutit (le gradient de la fonctionnelle a
suffisamment diminué), le minimum trouvé est une bonne
approximation de l'état initial réel puisqu'il est proche de
l'ébauche et des observations du système.
Sous-sections



suivant: 3D-VAR incrémental
monter: Assimilation variationnelle
précédent: Assimilation variationnelle
Table des matières
Retour à la page principale
![]() l'ébauche de la condition initiale,
l'ébauche de la condition initiale, ![]() le
vecteur des observations du système,
le
vecteur des observations du système, ![]() l'opérateur
d'observations permettant de relier un état
l'opérateur
d'observations permettant de relier un état ![]() du système aux
observations
du système aux
observations ![]() . La méthode du 3D-VAR (méthode variationnelle
à 3 dimensions) consiste à minimiser une fonction coût qui
mesure à la fois l'erreur sur la condition initiale et l'erreur sur
les observations :
. La méthode du 3D-VAR (méthode variationnelle
à 3 dimensions) consiste à minimiser une fonction coût qui
mesure à la fois l'erreur sur la condition initiale et l'erreur sur
les observations :