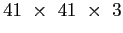
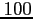
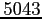
Dans cette partie (uniquement), nous avons réduit la dimension de notre problème afin d'étudier sur un problème de petite taille la perte d'équivalence entre les deux méthodes en passant du linéaire au non linéaire. Nous avons réduit la grille de discrétisation spatiale pour la ramener à une dimension de , soit un pas horizontal d'espace de km. La dimension de l'espace de contrôle est alors de . 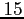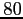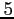Après une phase de spin-up de ans, la période d'assimilation débute et dure toujours pas de temps, soit jours. 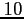L'ébauche considérée ici est l'état réel du système jours avant le début de la période d'assimilation. 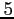Nous avons récupéré des observations à partir de la trajectoire exacte tous les pas de temps et d'espace. Nous ne les avons pas bruitées. La dimension de l'espace d'observation est alors de .

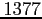
Dans un premier temps, nous avons comparé les deux méthodes sur le modèle linéarisé. Les fonctionnelles primale et duale sont alors strictement quadratiques, les modèles utilisés lors de la minimisation sont le modèle linéaire tangent et le modèle adjoint du linéaire tangent. Les méthodes primale et duale sont donc mathématiquement équivalentes et doivent conduire en théorie au même minimum. 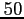Numériquement, et en arrêtant les minimisations après itérations pour les deux méthodes, les résultats diffèrent évidemment puisqu'aucun des deux algorithmes n'a eu le temps de converger vers le minimum, seulement de s'en approcher.

Figure 6.5: Évolution de l'erreur sur l'identification de la condition initiale en fonction du nombre d'itérations dans la minimisation, pour le problème linéarisé (a) et pour le problème non linéaire (b).

(a) (b)

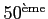
La figure 6.5-a montre la différence en norme RMS entre l'état initial reconstitué et l'état initial exact, pour chaque méthode, en fonction du nombre d'itérations dans la minimisation. On constate que même si la méthode duale fournit dès les premières itérations un meilleur résultat, assez vite, la méthode primale devient meilleure, pour le rester jusqu'à la itération. Celle-ci fournit globalement de meilleurs résultats que la méthode duale dans un cadre purement linéaire.

Nous avons ensuite appliqué les deux algorithmes sur le modèle non linéaire, en partant de la même ébauche que précédemment. Cette fois-ci, les méthodes ne sont plus mathématiquement équivalentes. La fig 6.5-b montre dans ce cas la différence en norme RMS entre l'état initial identifié par chacune des deux méthodes d'assimilation et l'état initial exact en fonction du nombre d'itérations dans l'algorithme de minimisation. Nous constatons que la méthode primale divise très rapidement par deux l'erreur sur la condition initiale avant de se stabiliser temporairement. La méthode duale fournit globalement de meilleurs résultats que la méthode primale dans le cadre non linéaire. La différence des résultats entre le modèle linéarisé et le modèle non linéaire s'explique par la perte d'équivalence des méthodes dans un cadre non linéaire et la méthode duale semble alors fournir de meilleurs résultats que la méthode primale.