Figure 6.18: Normes RMS des erreurs d'assimilation obtenues pour les deux méthodes en fonction de la dimension de l'espace des observations.

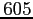
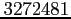
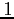
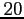
La figure 6.18 montre la norme RMS, moyennée sur toute la période d'assimilation, de l'erreur entre la solution identifiée et la trajectoire de référence en fonction du nombre d'observations disponibles. Celui varie de à en agissant sur la fréquence spatiale et temporelle de récupération des observations, qui varie elle de à . La courbe des erreurs commises avec la méthode primale est en trait plein et celle de la méthode duale en pointillés.

On constate plusieurs choses. Tout d'abord, lorsque le nombre d'observations disponibles est faible et a tendance à augmenter, l'erreur a tendance à dimniuer. En effet, plus on utilise d'observations et meilleure est l'assimilation de données. Néanmoins, à partir d'un grand nombre d'observations (plus que la dimension de l'espace des états), l'erreur a tendance à réaugmenter. Ceci provient essentiellement du fait que le système devient sur-déterminé (plus de données que d'inconnues), les données n'étant pas compatibles entre elles à cause notamment du bruitage.

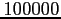
Si on compare les deux méthodes, on s'aperçoit que la méthode duale est meilleure lorsque le nombre d'observations est inférieur à , soit environ la dimension de l'espace des états. De plus, elle est un peu moins sensible à une diminution de la quantité d'informations. Ceci vient du fait que le nombre d'observations disponibles pour l'assimilation correspond à la dimension de l'espace de contrôle dual, et la minimisation de la fonction coût est alors beaucoup plus facile et poussée (pour un nombre d'itérations fixé dans l'algorithme de minimisation) ce qui conduit à de meilleurs résultats que la méthode primale. Cette dernière ne bénéficie que très peu de la diminution du nombre d'observations.

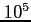
Lorsque le nombre d'observations est supérieur à , la méthode primale devient meilleure, ou plutôt la méthode duale devient un peu plus mauvaise. Ceci s'explique par un argument symétrique de celui que nous venons de voir pour un petit nombre d'observations. Ici, la dimension de l'espace de contrôle dual est supérieur à celle de l'espace primal. La minimisation est alors plus lente et délicate. De plus, le système devient surdéterminé, et ceci pose plus de problèmes à l'algorithme dual qu'au primal. En effet, la méthode duale est sous-déterminée puisque son vecteur de contrôle est de taille supérieure au nombre d'équations du modèle discrétisé, alors que la méthode primale est plutôt sur-déterminée (plus d'observations que d'inconnues) mais les données n'interviennent que dans la fonction coût et la sur-détermination du problème n'est pas vraiment gênante. Cela conduit juste à une fonctionnelle plus compliquée et donc un peu plus lente à minimiser a priori.

Il semble donc que l'algorithme dual soit légèrement moins sensible au nombre d'observations, et qu'il soit plus performant lorsque la dimension de l'espace des observations est plus petite que celle de l'espace des états. L'écart est assez flagrant lorsque le nombre d'observations utilisées pour l'assimilation est vraiment faible devant la dimension de l'espace des états puisque l'erreur d'assimilation de l'algorithme dual est jusqu'à environ deux fois plus faible que l'erreur commise avec la méthode primale.