Si on effectue un développement limité de
![]() au voisinage de
au voisinage de ![]() , on obtient :
, on obtient :
![$\displaystyle \begin{array}{lcl}
& & \nabla J(x_{k+1}) = \nabla J(x_k) + \nabl...
...x_k) +
\ldots [0.2cm]
(i.e.) & & y_k \approx \nabla^2J(x_k).s_k
\end{array} $](img223.png)
et donc, pour que
Par conséquent, il faudra effectuer avant (ou éventuellement après)
la mise à jour de la matrice diagonale une mise à l'échelle,
de sorte que la nouvelle matrice diagonale ait la bonne propriété.
Il conviendra donc de multiplier ![]() par
par
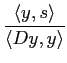 .
.
Cette mise à l'échelle permet d'économiser un certain nombre d'itérations et d'évaluations de la fonction coût et de son gradient [19].
L'impact de cette mise à jour sera étudié par la suite pour les trois premières formules de mise à jour du préconditionneur diagonal. En effet, cette mise à l'échelle n'a aucun sens dans le cas de la formule de quasi-Cauchy (3.6) puisque par construction, la nouvelle matrice diagonale vérifie déjà la condition (3.7).