


suivant: Justifications théoriques
monter: Présentation de la méthode
précédent: Présentation de la méthode
Table des matières
Considérons un problème d'évolution bien posé (ceci sera
assuré par certaines hypothèses que nous verrons plus loin) du
type :
![\begin{displaymath}\begin{array}{l} \displaystyle \frac{du}{dt}+A(t)u=f, \qquad 0\le t\le T, [0.4cm] u(0) = \xi, \end{array}\end{displaymath}](img278.png) |
(4.1) |
et cherchons la condition initiale 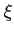 telle que la solution
telle que la solution 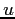 de
(4.1) vérifie la condition
de
(4.1) vérifie la condition 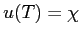 ,
, 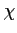 étant
la confition finale que l'on s'impose.
étant
la confition finale que l'on s'impose.
Généralement, le problème :
![\begin{displaymath}\begin{array}{l} \displaystyle \frac{du}{dt}+A(t)u=f, \qquad 0\le t\le T, [0.4cm] u(T) = \chi \end{array}\end{displaymath}](img282.png) |
(4.2) |
est mal posé et ne permet donc pas de résoudre notre problème.
Par contre, sous certaines hypothèses (à définir), le problème
![\begin{displaymath}\begin{array}{l} \displaystyle \frac{du_\varepsilon }{dt}+A(t...
...ad 0\le t\le T, [0.4cm] u_\varepsilon (T) = \chi \end{array}\end{displaymath}](img283.png) |
(4.3) |
admet une unique solution
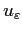 . Il est alors possible de définir une
suite de problèmes perturbés
. Il est alors possible de définir une
suite de problèmes perturbés
![\begin{displaymath}\begin{array}{l} \displaystyle \frac{dU_\varepsilon }{dt}+A(t...
..., [0.4cm] U_\varepsilon (0) = u_\varepsilon (0), \end{array}\end{displaymath}](img285.png) |
(4.4) |
et il convient de vérifier que
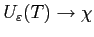 lorsque
lorsque
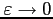 . Il ne restera qu'à choisir numériquement
. Il ne restera qu'à choisir numériquement
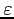 pour
avoir la précision voulue.
pour
avoir la précision voulue.



suivant: Justifications théoriques
monter: Présentation de la méthode
précédent: Présentation de la méthode
Table des matières
Retour à la page principale
![\begin{displaymath}\begin{array}{l} \displaystyle \frac{du}{dt}+A(t)u=f, \qquad 0\le t\le T, [0.4cm] u(0) = \xi, \end{array}\end{displaymath}](img278.png)