
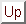


suivant: Application à l'équation de
monter: Présentation de la méthode
précédent: Heuristique
Table des matières
Soient 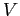 et
et 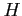 deux espaces de Hilbert avec
deux espaces de Hilbert avec
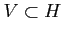 ,
, 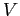 dense dans
dense dans 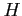 . On note
. On note 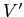 le dual de
le dual de 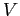 et on identifie
et on identifie 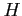 à son dual, de
sorte que
à son dual, de
sorte que
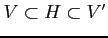 . On se donne à chaque instant
. On se donne à chaque instant
![$ t \in [0,T]$](img292.png) un
opérateur
un
opérateur
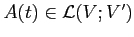 . On peut alors construire une famille de
formes bilinéaires
. On peut alors construire une famille de
formes bilinéaires 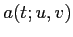 sur
sur 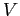 .
.
Supposons que 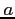 vérifie :
vérifie :
-
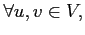 la fonction
la fonction
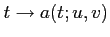 est mesurable.
est mesurable.
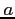 est uniformément continue sur
est uniformément continue sur
![$ [0,T] \times V \times V$](img298.png) :
:
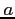 vérifie la propriété de coercivité élargie :
vérifie la propriété de coercivité élargie :
Alors nous avons les résultats suivants ([28]) :
Théorème 4.1
Soient
![$ f\in L^2([0,T],V')$](img301.png) et
et 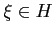 . Sous les hypothèses
énoncées précédemment sur
. Sous les hypothèses
énoncées précédemment sur 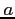 , il existe une unique solution
, il existe une unique solution
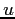 de (4.1) avec
de (4.1) avec
![$ u\in L^2([0,T],V)$](img303.png) et
et
![$ \displaystyle
\frac{du}{dt}\in L^2([0,T],V').\quad \blacksquare$](img304.png)
Notons 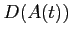 l'ensemble des fonctions acceptables en vue du problème
(4.3) :
l'ensemble des fonctions acceptables en vue du problème
(4.3) :
Théorème 4.2
Sous les hypothèses du théorème 4.1, en
supposant en outre que 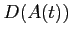 est un espace indépendant de
est un espace indépendant de 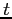 ,
alors le problème (4.3) admet une unique
solution
,
alors le problème (4.3) admet une unique
solution
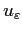 avec
avec
![$ u_\varepsilon \in L^2([0,T],D(A(t))$](img307.png) et
et
![$ \displaystyle
\frac{du_\varepsilon }{dt} \in L^2([0,T],D(A(t)).\quad \blacksquare$](img308.png)
Démonstration : Voir [24].

Nous avons désormais la possibilité de résoudre le problème
rétrograde perturbé. Intéressons nous à la convergence de la
suite de solutions ainsi construites :
Théorème 4.3
Sous les hypothèses du théorème 4.2, en supposant
de plus que la forme bilinéaire 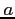 est indépendante du temps et
symétrique (i.e.
est indépendante du temps et
symétrique (i.e. 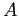 auto-adjoint), alors
auto-adjoint), alors
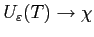 dans
dans 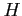 lorsque
lorsque
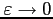 ,
,
![$ U_\varepsilon \in L^2([0,T],V)$](img311.png) étant défini par
(4.4).
étant défini par
(4.4).
Démonstration : Voir [24] et [6].

La convergence de la suite des états finaux
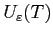 vers l'état
final de référence
vers l'état
final de référence 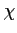 est acquise, mais la convergence de la
suite
est acquise, mais la convergence de la
suite
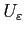 en n'importe quel autre point de
en n'importe quel autre point de ![$ [0,T]$](img315.png) n'a
généralement pas lieu d'être. Nous allons maintenant appliquer
numériquement la méthode de la quasi-réversibilité à
l'équation de la chaleur.
n'a
généralement pas lieu d'être. Nous allons maintenant appliquer
numériquement la méthode de la quasi-réversibilité à
l'équation de la chaleur.



suivant: Application à l'équation de
monter: Présentation de la méthode
précédent: Heuristique
Table des matières
Retour à la page principale
![]() et
et ![]() deux espaces de Hilbert avec
deux espaces de Hilbert avec
![]() ,
, ![]() dense dans
dense dans ![]() . On note
. On note ![]() le dual de
le dual de ![]() et on identifie
et on identifie ![]() à son dual, de
sorte que
à son dual, de
sorte que
![]() . On se donne à chaque instant
. On se donne à chaque instant
![]() un
opérateur
un
opérateur
![]() . On peut alors construire une famille de
formes bilinéaires
. On peut alors construire une famille de
formes bilinéaires ![]() sur
sur ![]() .
.
![]() vérifie :
vérifie :
![$ \displaystyle
\frac{du}{dt}\in L^2([0,T],V').\quad \blacksquare$](img304.png)
![]() l'ensemble des fonctions acceptables en vue du problème
(4.3) :
l'ensemble des fonctions acceptables en vue du problème
(4.3) :
![$ \displaystyle
\frac{du_\varepsilon }{dt} \in L^2([0,T],D(A(t)).\quad \blacksquare$](img308.png)
![]() vers l'état
final de référence
vers l'état
final de référence ![]() est acquise, mais la convergence de la
suite
est acquise, mais la convergence de la
suite
![]() en n'importe quel autre point de
en n'importe quel autre point de ![]() n'a
généralement pas lieu d'être. Nous allons maintenant appliquer
numériquement la méthode de la quasi-réversibilité à
l'équation de la chaleur.
n'a
généralement pas lieu d'être. Nous allons maintenant appliquer
numériquement la méthode de la quasi-réversibilité à
l'équation de la chaleur.