Le principe de l'interpolation optimale est de chercher une
combinaison linéaire optimale entre les observations et les états
du système aux mêmes instants. L'estimateur qui réalise le
minimum de la variance de l'erreur d'estimation est alors appelé
BLUE, Best Linear Unbiaised Estimator ([42], [31],
[12], [36]). Si on note ![]() (background ou ébauche) une estimation de l'état du système
(background ou ébauche) une estimation de l'état du système ![]() avant assimilation de données, et
avant assimilation de données, et ![]() (analysis ou état
analysé) le BLUE, le but est de chercher le meilleur terme correctif
à
(analysis ou état
analysé) le BLUE, le but est de chercher le meilleur terme correctif
à ![]() en fonction du vecteur d'innovation, le vecteur
en fonction du vecteur d'innovation, le vecteur ![]() , qui
représente l'écart entre les observations et l'état
correspondant du système.
, qui
représente l'écart entre les observations et l'état
correspondant du système.
Il y a deux façons de trouver cette meilleure estimation. La première repose essentiellement sur des considérations statistiques et l'autre plutôt sur la minimisation d'une fonctionnelle, mais ces deux approches sont en fait très comparables. Étudions tout d'abord l'approche statistique.
Étant données deux variables aléatoires ![]() et
et ![]() d'espérances
mathématiques respectives
d'espérances
mathématiques respectives ![]() et
et ![]() , la meilleure estimation
linéaire de
, la meilleure estimation
linéaire de ![]() à partir de
à partir de ![]() (qui minimise la variance de
l'erreur d'estimation) est :
(qui minimise la variance de
l'erreur d'estimation) est :
Il apparaît alors que ![]() est la projection orthogonale (au
sens de la covariance statistique) de
est la projection orthogonale (au
sens de la covariance statistique) de ![]() sur l'espace vectoriel engendré
par
sur l'espace vectoriel engendré
par ![]() , et par conséquent,
, et par conséquent, ![]() et
et ![]() sont orthogonaux et donc
décorrélés.
sont orthogonaux et donc
décorrélés.
Nous allons désormais considérer que ![]() est relié à l'ébauche
est relié à l'ébauche ![]() par une relation linéaire de la forme
par une relation linéaire de la forme ![]() ,
, ![]() pouvant être considéré
comme un opérateur d'observation servant à relier les états du système
pouvant être considéré
comme un opérateur d'observation servant à relier les états du système
![]() aux observations
aux observations ![]() .
En notant
.
En notant
![]() la
matrice de covariance de l'erreur d'ébauche, et
la
matrice de covariance de l'erreur d'ébauche, et
![]() la matrice de covariance d'erreur
d'observation, et en supposant que les erreurs d'ébauche et d'observation sont
décorrélées, on peut réécrire (2.2) sous la forme
suivante :
la matrice de covariance d'erreur
d'observation, et en supposant que les erreurs d'ébauche et d'observation sont
décorrélées, on peut réécrire (2.2) sous la forme
suivante :
L'équation (2.3) donne le meilleur estimateur possible (le
BLUE) de ![]() connaissant le vecteur d'ébauche
connaissant le vecteur d'ébauche ![]() , le
vecteur d'innovation
, le
vecteur d'innovation ![]() et les matrices de covariance des
erreurs relatives à l'estimation de l'état réel
et les matrices de covariance des
erreurs relatives à l'estimation de l'état réel ![]() et aux
mesures des observations
et aux
mesures des observations ![]() .
.
Si on s'intéresse au même problème, mais en essayant de
quantifier l'écart du vecteur d'état ![]() par rapport à
par rapport à ![]() et
celui de l'observation
et
celui de l'observation ![]() par rapport à
par rapport à ![]() , nous pouvons
introduire la fonction coût suivante :
, nous pouvons
introduire la fonction coût suivante :
La première partie de la fonctionnelle ![]() mesure l'écart au sens
des moindres carrés (via la matrice de covariance d'erreur
d'ébauche) entre l'état du système
mesure l'écart au sens
des moindres carrés (via la matrice de covariance d'erreur
d'ébauche) entre l'état du système ![]() et l'ébauche
et l'ébauche ![]() . Le
second terme mesure de la même façon l'écart aux
observations. Le minimum d'une telle fonction coût devrait ainsi
être proche à la fois de l'ébauche et des observations.
. Le
second terme mesure de la même façon l'écart aux
observations. Le minimum d'une telle fonction coût devrait ainsi
être proche à la fois de l'ébauche et des observations.
En supposant l'opérateur d'observation ![]() linéaire, la fonctionnelle
linéaire, la fonctionnelle
![]() est strictement convexe et son minimum est alors atteint lorsque
son gradient est nul :
est strictement convexe et son minimum est alors atteint lorsque
son gradient est nul :
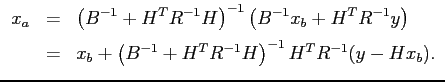
Un calcul rapide portant sur la matrice de gain
Cette méthode est relativement rapide, puisqu'il suffit de multiplier
le vecteur d'innovation par une matrice (matrice de gain) pour
obtenir le terme correctif à apporter à l'ébauche pour trouver
la meilleure estimation linéaire de l'état réel du système.
Ceci dit, elle repose essentiellement sur la connaissance des deux
matrices de covariance d'erreur, ce qui est loin d'être le cas,
ainsi que sur la linéarité de l'opérateur d'observation ![]() ,
ce qui n'est pas toujours vrai. Enfin, la taille des matrices n'est pas
sans poser quelques difficultés numériques.
,
ce qui n'est pas toujours vrai. Enfin, la taille des matrices n'est pas
sans poser quelques difficultés numériques.