![$\displaystyle \left\{ \begin{array}{l} x_0 \textrm{ donn\'e,} [0.2cm] x_{n+1} = M_n x_n + \varepsilon_n, \quad n \ge 0, \end{array} \right.$](img69.png) |
(2.7) |
Nous allons désormais nous pencher sur la technique du filtrage de Kalman ([22], [16], [17], [18], [20], [15], [14], [8], [52]). Cette théorie fournit à chaque nouvelle observation une nouvelle estimation de la variable d'état. Le filtrage de Kalman utilise les observations dans l'ordre où elles sont disponibles, d'où l'appellation séquentielle. Par conséquent, l'estimation de l'état du système ne dépendra pas des observations futures mais uniquement des observations passées et présentes.
Considérons une discrétisation en temps de notre problème :
On doit également discrétiser en temps les observations :
Notons, à chaque instant ![]() ,
, ![]() et
et ![]() les matrices de
covariance des erreurs de modèle et d'observation respectivement.
Nous supposerons dans la suite que ces deux erreurs sont d'espérance
nulle et décorrélées (l'une par rapport à l'autre et entre elles
à des instants différents).
les matrices de
covariance des erreurs de modèle et d'observation respectivement.
Nous supposerons dans la suite que ces deux erreurs sont d'espérance
nulle et décorrélées (l'une par rapport à l'autre et entre elles
à des instants différents).
L'ébauche de l'état du système à l'instant ![]() n'est autre
que l'état obtenu en faisant évoluer l'analyse réalisée à
l'instant d'avant sur un pas de temps :
n'est autre
que l'état obtenu en faisant évoluer l'analyse réalisée à
l'instant d'avant sur un pas de temps :
Si on note ![]() la matrice de covariance de l'erreur d'ébauche
la matrice de covariance de l'erreur d'ébauche
![]() et
et ![]() la matrice de covariance de l'erreur d'analyse
la matrice de covariance de l'erreur d'analyse
![]() , alors
, alors
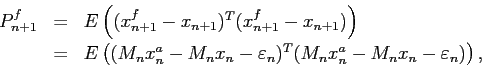
donc
Cette phase est appelée la phase de prédiction : on a déduit une
estimation de l'état à l'instant ![]() de la prévision de
l'instant
de la prévision de
l'instant ![]() , ainsi que la matrice de covariance de l'erreur d'ébauche
en fonction de la matrice de covariance de l'erreur d'analyse de l'instant
précédent.
, ainsi que la matrice de covariance de l'erreur d'ébauche
en fonction de la matrice de covariance de l'erreur d'analyse de l'instant
précédent.
À partir de cette ébauche et du vecteur d'innovation
![]() , il faut construire l'état analysé
, il faut construire l'état analysé
![]() , de façon analogue à la méthode de l'interpolation
optimale :
, de façon analogue à la méthode de l'interpolation
optimale :
Les équations (2.11) et (2.12) ne sont pas sans rappeler l'équation (2.6) qui donnait l'analyse en fonction de l'ébauche dans le cadre de l'interpolation optimale, sauf qu'ici la dépendance du temps intervient dans chaque matrice et chaque vecteur.
Il est alors aisé de calculer la nouvelle matrice de covariance d'erreur d'analyse :
Cette phase est appelée la phase de correction : on a corrigé l'estimation fournie par l'étape de prédiction à l'aide du vecteur d'innovation et d'une matrice de gain.
Il faut noter que la matrice de covariance d'erreur d'analyse ![]() est
indépendante des valeurs des observations, contrairement à l'état
analysé
est
indépendante des valeurs des observations, contrairement à l'état
analysé ![]() .
.
Le gros avantage de la méthode du filtre de Kalman est de fournir
à chaque itération une estimation des matrices de covariance
d'erreur d'ébauche et d'analyse. Il faut toutefois initialiser
correctement ces matrices à l'instant ![]() , et avoir une estimation
des matrices de covariance d'erreur modèle et d'erreur
d'observation. Cependant, en météorologie, l'initialisation
n'est pas une difficulté majeure car les observations s'accumulent
dans le temps, et en pratique, la mise en route de l'algorithme de
filtrage est assez vite oubliée.
, et avoir une estimation
des matrices de covariance d'erreur modèle et d'erreur
d'observation. Cependant, en météorologie, l'initialisation
n'est pas une difficulté majeure car les observations s'accumulent
dans le temps, et en pratique, la mise en route de l'algorithme de
filtrage est assez vite oubliée.
Plusieurs inconvénients majeurs sont cependant connus. Tout d'abord, dans le cas d'un modèle non linéaire, le filtre de Kalman ainsi défini n'est pas optimal (il ne fournit pas la solution de variance minimale). Pour pallier à ce défaut qui pose problème dès qu'on utilise le filtre de Kalman sur un problème même faiblement non linéaire, a été introduit le filtre de Kalman étendu qui travaille à chaque instant sur des versions linéarisées du modèle (système linéaire tangent) et de l'opérateur d'observation (opérateur linéaire tangent d'observation). Ainsi, dans le cas d'un modèle linéaire, il est optimal, et dans le cas d'un modèle non linéaire, même s'il n'est pas forcément optimal, il donne de bonnes analyses si les non linéarités ne sont pas trop importantes.
Le second problème qui se pose est le coût de la mise en ![]() uvre
numérique du filtre de Kalman. En effet, si la dimension du problème
est de l'ordre de
uvre
numérique du filtre de Kalman. En effet, si la dimension du problème
est de l'ordre de ![]() , et la dimension des observations de l'ordre de
, et la dimension des observations de l'ordre de
![]() , les matrices
, les matrices ![]() ,
, ![]() ,
, ![]() et
et ![]() sont des matrices
carrées de dimension
sont des matrices
carrées de dimension
![]() , la matrice
, la matrice ![]() est carrée
de dimension
est carrée
de dimension
![]() et les matrices
et les matrices ![]() et
et ![]() sont
rectangulaires de dimension
sont
rectangulaires de dimension
![]() .
Le stockage d'une matrice de cet ordre de grandeur pose problème, mais
il n'est heureusement pas utile, car seul le résultat de la
multiplication d'une telle matrice par un vecteur est nécessaire.
Pour des raisons évidentes de coût de calcul, il est nécessaire
de réduire la dimension du filtre si on veut l'appliquer à des
problèmes d'océanographie ou météorologie.
.
Le stockage d'une matrice de cet ordre de grandeur pose problème, mais
il n'est heureusement pas utile, car seul le résultat de la
multiplication d'une telle matrice par un vecteur est nécessaire.
Pour des raisons évidentes de coût de calcul, il est nécessaire
de réduire la dimension du filtre si on veut l'appliquer à des
problèmes d'océanographie ou météorologie.