


suivant: Classification
monter: Restauration
précédent: Remarques
Table des matières
Il existe plusieurs façons de considérer une image en couleur. En utilisant un espace adapté pour la représentation multi-dimensionnelle, par exemple l'espace RGB (rouge-vert-bleu), l'image en couleur peut être modélisée par une fonction de 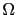 dans
dans
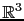 au lieu de
au lieu de
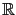 . Une première approche consiste à découpler les canaux, et résoudre un problème direct et un problème adjoint pour chacun des canaux. Mais ces équations peuvent également être résolues directement de façon vectorielle pour identifier les images vectorielles
. Une première approche consiste à découpler les canaux, et résoudre un problème direct et un problème adjoint pour chacun des canaux. Mais ces équations peuvent également être résolues directement de façon vectorielle pour identifier les images vectorielles 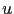 et
et 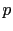 . Le développement asymptotique topologique reste donné par les équations (2.25-2.26) et (2.28), où les fonctions impliquées sont vectorielles, i.e. le gradient topologique vectoriel est la somme des expressions correspondant à chacun des canaux [26].
. Le développement asymptotique topologique reste donné par les équations (2.25-2.26) et (2.28), où les fonctions impliquées sont vectorielles, i.e. le gradient topologique vectoriel est la somme des expressions correspondant à chacun des canaux [26].
Une autre approche a été étudiée dans [26], en utilisant une norme qui permet de coupler les différents canaux entre eux. Dans l'approche définie par Di Zenzo [57], l'idée consiste à considérer le tenseur de structure
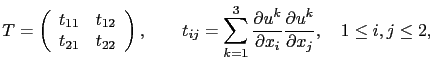 |
(2.30) |
dans le cas d'images bi-dimensionnelles. Ce tenseur décrit la structure différentielle de l'image, et le gradient de Di Zenzo est défini par la plus grande valeur propre de ce tenseur:
![$\displaystyle \Vert\nabla u\Vert _{DZ} = \frac{1}{\sqrt{2}} \left[ t_{11}+t_{22}+\sqrt{(t_{11}-t_{22})^2+4t_{12}^2}\right]^{\frac{1}{2}}.$](img130.png) |
(2.31) |
Grâce à une réécriture du gradient à l'aide de la fonction suivante:
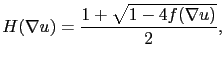 |
(2.32) |
avec
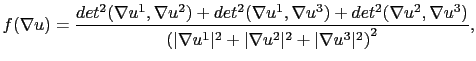 |
(2.33) |
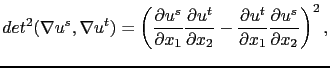 |
(2.34) |
il est possible de dériver le développement asymptotique de la fonction coût définie par l'équation (2.24) dans laquelle la norme utilisée est celle définie en (2.31):
![$\displaystyle G(x_0,n) = \sum_{k=1}^3 \left[ -\pi c (\nabla u_0^k(x_0).n)(\nabla v_0^k(x_0).n)-\pi H(\nabla u_0(x_0))\vert\nabla u_0^k(x_0).n\vert^2\right]$](img134.png) |
(2.35) |
en utilisant les mêmes notations que précédemment.
Dans [26], nous montrons que cette approche a le même coût de calcul que l'algorithme où les différents canaux sont découplés, alors qu'il permet d'améliorer la détection des contours de l'image, et par conséquent d'obtenir une image restaurée plus précise aux abords des contours de l'image.

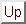


suivant: Classification
monter: Restauration
précédent: Remarques
Table des matières
Retour à la page principale
![]() dans
dans
![]() au lieu de
au lieu de
![]() . Une première approche consiste à découpler les canaux, et résoudre un problème direct et un problème adjoint pour chacun des canaux. Mais ces équations peuvent également être résolues directement de façon vectorielle pour identifier les images vectorielles
. Une première approche consiste à découpler les canaux, et résoudre un problème direct et un problème adjoint pour chacun des canaux. Mais ces équations peuvent également être résolues directement de façon vectorielle pour identifier les images vectorielles ![]() et
et ![]() . Le développement asymptotique topologique reste donné par les équations (2.25-2.26) et (2.28), où les fonctions impliquées sont vectorielles, i.e. le gradient topologique vectoriel est la somme des expressions correspondant à chacun des canaux [26].
. Le développement asymptotique topologique reste donné par les équations (2.25-2.26) et (2.28), où les fonctions impliquées sont vectorielles, i.e. le gradient topologique vectoriel est la somme des expressions correspondant à chacun des canaux [26].
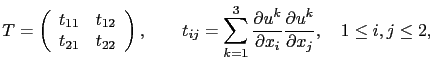
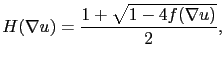
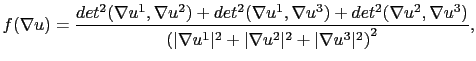
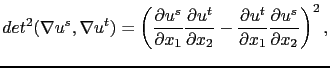
![$\displaystyle G(x_0,n) = \sum_{k=1}^3 \left[ -\pi c (\nabla u_0^k(x_0).n)(\nabla v_0^k(x_0).n)-\pi H(\nabla u_0(x_0))\vert\nabla u_0^k(x_0).n\vert^2\right]$](img134.png)