next up previous contents
suivant: Complexité des algorithmes monter: Segmentation précédent: Développement en série entière   Table des matières

Algorithme

On peut alors définir l'algorithme suivant, basé en partie sur l'algorithme de restauration défini en section 2.4:

$ \bullet$
Résoudre les problèmes direct (2.21) et adjoint (2.27) non perturbés (i.e. avec 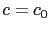$ c=c_0$ partout).
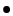
$ \bullet$
Assembler la matrice 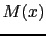$ M(x)$ définie par (2.28) et calculer la valeur propre
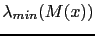$ \lambda_{min}(M(x))$ la plus négative en chaque point du domaine.
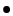
$ \bullet$
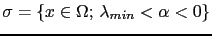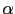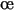Définir l'ensemble des contours: $ \sigma=\left\{ x\in\Omega; \lambda_{min}<\alpha<0\right\}$ où $ \alpha$ est un c\oefficient de seuillage négatif.
$ \bullet$
Définir la valeur critique 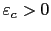$ \varepsilon_c>0$ en dessous de laquelle la résolution numérique du problème 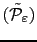$ (\tilde{\mathcal{P}}_\varepsilon)$ est difficile.
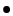
$ \bullet$
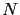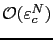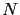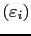Choisir le degré $ N$ de l'approximation pour que la norme du résidu soit en $ \mathcal{O}(\varepsilon_c^N)$ , et $ N$ valeurs différentes $ (\varepsilon_i)$ .
$ \bullet$
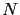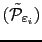Résoudre les $ N$ problèmes $ (\tilde{\mathcal{P}}_{\varepsilon_i})$ .
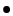
$ \bullet$
Calculer la valeur en 0 du polynôme d'interpolation 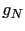$ g_N$ défini par (2.52).

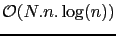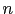La complexité de cet algorithme est donc en $ \mathcal{O}(N.n.\log(n))$ , où $ n$ est le nombre de pixels de l'image, et 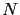$ N$ est le degré de l'approximation par interpolation. Typiquement, dans les tests numériques, 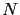$ N$ est de l'ordre de 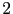$ 2$ à $ 5$ .

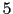Des tests numériques ont été réalisés pour montrer l'intérêt de cet algorithme, et sont présentés dans [19].

next up previous contents
suivant: Complexité des algorithmes monter: Segmentation précédent: Développement en série entière   Table des matières
Retour à la page principale