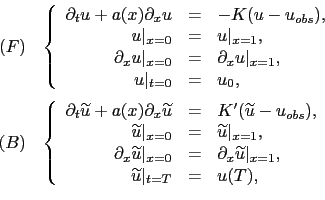Transport linéaire non visqueux

On considère désormais le cas non visqueux des équations de transport linéaire. Les équations du BFN sont:

Théorème 3.5 On considère une itération du BFN sur le modèle (3.32), avec des observations $u_{obs}$ qui vérifient l'équation (3.32-F) avec . On note

$\begin{displaymath}\begin{array}{rcl} w(t) &=& u(t) - u_{obs}(t), \widetilde{w}(t) &=& \widetilde{u}(t)-u_{obs}(t). \end{array}\end{displaymath}$

(3.33)

Soit

$\displaystyle (s,\psi(s,x))$

(3.34)

la courbe caractéristique associée à l'équation (3.32-F) avec , issue de à l'instant , i.e. telle que

$\displaystyle (s,\psi(s,x))\vert _{s=0} = (0,x).$

(3.35)

On suppose que le temps final est tel que les caractéristiques sont bien définies et ne se croisent pas sur . Alors nous avons les résultats suivants:

Si , alors pour tout $t\in[0,T]$ ,

$\displaystyle \widetilde{w}(t) = w(t) e^{(-K-K^\prime)(T-t)}.$ (3.36)
Si $K(t,x)=K \mathbbm{1}_{[t_{1},t_{2}]}(t)$ avec $0\leq t_{1} < t_{2}\leq T$ , alors

$\displaystyle \widetilde{w}(0) = w(0) e^{(-K-K^\prime)(t_{2}-t_{1})}.$ (3.37)
Si , alors pour tout $t\in[0,T]$ ,

$\displaystyle \widetilde{w}(t,\psi(t,x)) = w(t,\psi(t,x)) \exp \left(-\int_{t}^T K(\psi(s,x))+K^\prime(\psi(s,x)) ds \right).$ (3.38)

On en déduit que dans le cas où le terme de rappel agit sur tout le domaine (cas

du théorème précédent), l'algorithme BFN converge pour les équations de transport linéaire non visqueux. De plus, dans le cas où le support de

ne recouvre pas tout le domaine (cas

, par exemple lorsque les observations sont partielles), l'algorithme converge dès que toutes les courbes caractéristiques rencontrent le support de

, ce qui est par exemple garanti par l'observabilité du système (voir les remarques après la proposition 3.2 ci-dessous).