


suivant: Étude d'une classe d'observateurs
monter: Lien avec les observateurs
précédent: Observateurs pour un modèle
Table des matières
Le modèle shallow water que nous considérons est invariant par rotation et translation, puisqu'il ne dépend ni de l'orientation, ni de l'origine du repère. Par conséquent, nous allons chercher des termes de rappel qui conservent ces invariances. La conception d'observateurs invariants (ou qui préservent les symétries du modèle) a été très récemment introduite, essentiellement pour des problèmes industriels [2,41]. L'idée sous-jacente est évidemment de ne pas perturber les symétries du modèle lors de l'ajout du terme de rappel vers les données dans les équations de l'observateur.
Pour le terme scalaire portant sur la hauteur d'eau, un résultat de calcul différentiel assure que tout opérateur différentiel scalaire invariant par rotation et translation s'écrit comme un polynôme du Laplacien [99]. Par des considérations d'invariance par rotation [88], on arrive ainsi à une famille d'opérateurs scalaires de la forme
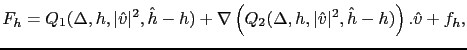 |
(3.52) |
où 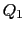 et
et 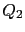 sont deux polynômes scalaires du Laplacien, et
sont deux polynômes scalaires du Laplacien, et 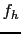 est un terme intégral. Plus précisément,
est un terme intégral. Plus précisément,
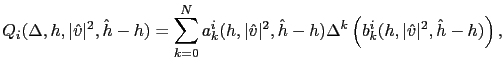 |
(3.53) |
où 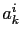 et
et 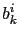 sont des fonctions scalaires régulières qui s'annulent lorsque le troisième argument est nul. De même, le terme de rappel vectoriel sur la vitesse est de la forme
sont des fonctions scalaires régulières qui s'annulent lorsque le troisième argument est nul. De même, le terme de rappel vectoriel sur la vitesse est de la forme
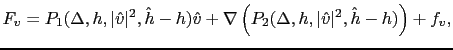 |
(3.54) |
où les polynômes 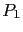 et
et 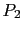 sont du même type que
sont du même type que 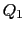 et
et 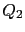 .
.
On définit alors les termes intégraux 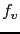 et
et 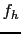 de sorte qu'ils soient eux aussi invariants par rotation et translation. On obtient ainsi les formulations suivantes:
de sorte qu'ils soient eux aussi invariants par rotation et translation. On obtient ainsi les formulations suivantes:
![$\displaystyle f_v(x,y,t)=\iint \left[ R_1(\Delta,h,\vert\hat{v}\vert^2,\hat{h}-...
...t{h}-h)\right) \right]_{(x-\xi,y-\zeta,t)} \phi_v(\xi^2+\zeta^2) d\xi d\zeta,$](img394.png) |
(3.55) |
![$\displaystyle f_h(x,y,t)=\iint \left[ S_1(\Delta,h,\vert\hat{v}\vert^2,\hat{h}-...
...right).\hat{v} \right]_{(x-\xi,y-\zeta,t)} \phi_h(\xi^2+\zeta^2) d\xi d\zeta,$](img395.png) |
(3.56) |
où les polynômes 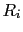 et
et 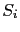 sont définis commes les polynômes
sont définis commes les polynômes 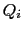 et
et 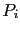 .
.
Les supports de 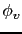 et
et 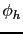 permettent de définir une zone d'influence où cela a un sens de corriger l'observateur avec les valeurs observées. Dans le cas particulier où ces fonctions sont des fonctions Dirac, alors les fonctions
permettent de définir une zone d'influence où cela a un sens de corriger l'observateur avec les valeurs observées. Dans le cas particulier où ces fonctions sont des fonctions Dirac, alors les fonctions 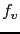 et
et 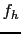 deviennent équivalentes aux autres termes de
deviennent équivalentes aux autres termes de 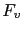 et
et 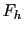 .
.



suivant: Étude d'une classe d'observateurs
monter: Lien avec les observateurs
précédent: Observateurs pour un modèle
Table des matières
Retour à la page principale
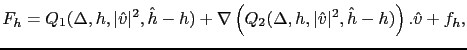
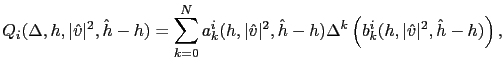
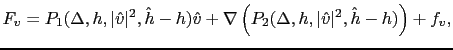
![]() et
et ![]() de sorte qu'ils soient eux aussi invariants par rotation et translation. On obtient ainsi les formulations suivantes:
de sorte qu'ils soient eux aussi invariants par rotation et translation. On obtient ainsi les formulations suivantes:
![$\displaystyle f_v(x,y,t)=\iint \left[ R_1(\Delta,h,\vert\hat{v}\vert^2,\hat{h}-...
...t{h}-h)\right) \right]_{(x-\xi,y-\zeta,t)} \phi_v(\xi^2+\zeta^2) d\xi d\zeta,$](img394.png)
![$\displaystyle f_h(x,y,t)=\iint \left[ S_1(\Delta,h,\vert\hat{v}\vert^2,\hat{h}-...
...right).\hat{v} \right]_{(x-\xi,y-\zeta,t)} \phi_h(\xi^2+\zeta^2) d\xi d\zeta,$](img395.png)
![]() et
et ![]() permettent de définir une zone d'influence où cela a un sens de corriger l'observateur avec les valeurs observées. Dans le cas particulier où ces fonctions sont des fonctions Dirac, alors les fonctions
permettent de définir une zone d'influence où cela a un sens de corriger l'observateur avec les valeurs observées. Dans le cas particulier où ces fonctions sont des fonctions Dirac, alors les fonctions ![]() et
et ![]() deviennent équivalentes aux autres termes de
deviennent équivalentes aux autres termes de ![]() et
et ![]() .
.