next up previous contents
suivant: Expériences numériques monter: Lien avec les observateurs précédent: Utilisation des symétries du   Table des matières

Étude d'une classe d'observateurs dans un cas linéarisé

Nous considérons maintenant un cas simple, où on ne garde que les termes intégraux des termes de correction: $ Q_1=Q_2=P_1=P_2=0$ , $ R_1=S_2=0$ et $ S_2=R_1=h-\hat{h}$ . En effet, les mesures de la hauteur d'eau étant généralement bruitées, on ne souhaite pas les dériver, ce qui amplifierait considérablement le bruit.

Sans perdre en généralité, on peut également simplifier les équations du modèle (pas de force de Coriolis, pas de friction ou dissipation par viscosité, pas de forçage par le vent, ...). L'observateur pour le système simplifié est alors:

$\displaystyle \frac{\partial \hat{h}}{\partial t}$ $\displaystyle =$ $\displaystyle -\nabla(\hat{h}\hat{v})+\phi_h \ast (h-\hat{h}),$ (3.57)
$\displaystyle \frac{\partial \hat{v}}{\partial t}$ $\displaystyle =$ $\displaystyle -\hat{v}\nabla \hat{v}-g\nabla \hat{h}+\phi_v\ast\nabla(h-\hat{h}).$ (3.58)

Dans le cas dégénéré où $ \phi_h=K_h\delta_0$ et $ \phi_v=K_v\delta_0$ , $ K_h$ et $ K_v$ étant des scalaires positifs et $ \delta_0$ représentant la mesure de Dirac en 0 , les équations (3.57-3.58) deviennent la formulation classique du nudging (ou observateur de Luenberger).

On suppose par ailleurs que le système est proche d'un état d'équilibre, et on ne considèrera que des petites vitesses $ \delta v = v-\bar{v} \ll \sqrt{g\bar{h}}$ et $ \delta h = h - \bar{h} \ll \bar{h}$ , où $ \bar{h}$ et $ \bar{v}=0$ représentent respectivement la hauteur d'eau et vitesse du fluide au point d'équilibre. En notant $ \tilde{h}$ et $ \tilde{v}$ l'écart (sur la hauteur d'eau et la vitesse respectivement) entre l'observateur et la solution réelle du système simplifié et linéarisé, alors ces erreurs d'estimation vérifient les équations linéaires suivantes:

$\displaystyle \frac{\partial \tilde{h}}{\partial t}$ $\displaystyle =$ $\displaystyle -\bar{h}\nabla \tilde{v}-\phi_h \ast \tilde{h},$ (3.59)
$\displaystyle \frac{\partial \tilde{v}}{\partial t}$ $\displaystyle =$ $\displaystyle -g\nabla \tilde{h} -\phi_v \ast \nabla \tilde{h}.$ (3.60)

Un choix raisonnable pour les fonctions $ \phi_h$ et $ \phi_v$ consiste à prendre des noyaux gaussiens de la forme:

$\displaystyle \phi_h(x,y)$ $\displaystyle =$ $\displaystyle \beta_h exp(-\alpha_h (x^2+y^2)),$ (3.61)
$\displaystyle \phi_v(x,y)$ $\displaystyle =$ $\displaystyle \beta_v exp(-\alpha_v (x^2+y^2)),$ (3.62)

puisqu'on suppose généralement que les mesures sont entachées d'un bruit blanc gaussien. Toutefois, les résultats de convergence obtenus ci-dessous peuvent s'étendre au cas de noyaux qui s'écrivent sous la forme:
$\displaystyle \phi_h(x,y)$ $\displaystyle =$ $\displaystyle (f(x)\ast f(x)) (f(y)\ast f(y)),$ (3.63)
$\displaystyle \phi_v(x,y)$ $\displaystyle =$ $\displaystyle (g(x)\ast g(x)) (g(y)\ast g(y)),$ (3.64)

où $ f$ et $ g$ sont des fonctions lisses (par exemple $ C^\infty$ ), et dont les c\oefficients de Fourier sont réels et strictement positifs.

En éliminant la vitesse du système d'équations (3.59-3.60), la hauteur vérifie l'équation suivante:

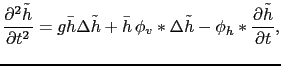$\displaystyle \frac{\partial^2 \tilde{h}}{\partial t^2} = g\bar{h}\Delta \tilde... ...h} \phi_v\ast\Delta\tilde{h} - \phi_h\ast\frac{\partial\tilde{h}}{\partial t},$ (3.65)

qui s'apparente à une équation des ondes amortie, avec un amortissement visqueux externe. Cette équation peut être réécrite sous la forme suivante:

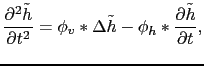$\displaystyle \frac{\partial^2 \tilde{h}}{\partial t^2} = \phi_v\ast\Delta\tilde{h} - \phi_h\ast\frac{\partial\tilde{h}}{\partial t},$ (3.66)

en redéfinissant

$\displaystyle \phi_v(x,y) = g\bar{h}\delta_0 + \bar{h} \beta_v exp(-\alpha_v (x^2+y^2)),$ (3.67)

où $ \delta_0$ représente la mesure de Dirac en 0 .

Dans ces conditions, nous avons le résultat suivant [23]:

Théorème 3.7  

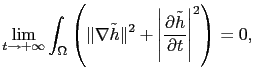$\displaystyle \lim_{t\to +\infty} \int_\Omega \left( \Vert\nabla \tilde{h}\Vert^2 + \left\vert\frac{\partial \tilde{h}}{\partial t}\right\vert^2 \right) = 0,$ (3.68)

qui montre la convergence forte de l'erreur vers 0 pour le système linéarisé, et donc de l'observateur vers la solution réelle. La convergence est alors étendue sans difficulté à la vitesse $ v$ .

Une analyse dimensionnelle permet également de prédire les valeurs typiques des c\oefficients de gain des fonctions $ \phi_h$ et $ \phi_v$ (cf équations (3.61) et (3.68)):

$\displaystyle \beta_h = 2\xi_0\omega_0, \quad \bar h\beta_v = L_0^2\omega_0^2-g\bar{h},$ (3.69)

où $ \omega_0$ et $ L_0$ représentent respectivement la pulsation et la taille caractéristiques de l'écoulement, et $ \xi_0$ représente le c\oefficient d'amortissement du système. De même, les c\oefficients $ \alpha_h$ et $ \alpha_v$ peuvent être déterminés a priori, en imposant $ \alpha_h^{-2}=\alpha_v^{-2}$ , cette valeur étant égale à la taille caractéristique de la région d'influence des observations. Cette dernière dépend essentiellement de la quantité de bruit sur les mesures, mais aussi de la répartition spatiale des données.

next up previous contents
suivant: Expériences numériques monter: Lien avec les observateurs précédent: Utilisation des symétries du   Table des matières
Retour à la page principale