Notons ![]() la solution du modèle direct sans erreur modèle
et sans incertitude sur la condition initiale :
la solution du modèle direct sans erreur modèle
et sans incertitude sur la condition initiale :
En vue de considérer des équations matricielles, on notera dans la
suite ![]() le vecteur comprenant toutes les observations :
le vecteur comprenant toutes les observations :
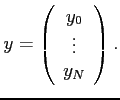
On notera
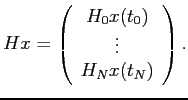
On note
comme étant l'écart entre les observations et la solution de référence du problème. On note enfin
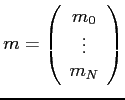
un vecteur quelconque de l'espace des observations. En étudiant le système d'optimalité (5.25), on constate qu'il faut considérer le vecteur d'observation
L'algorithme dual est alors le suivant :
On a alors la proposition suivante :
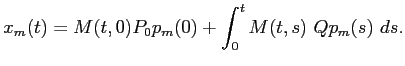
Par transposition, on obtient que la résolvante du système associée à
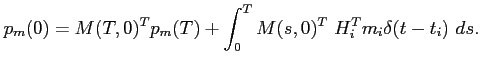
Choisissons un vecteur
On a donc
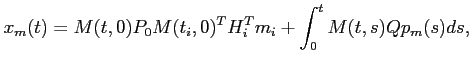
On a donc
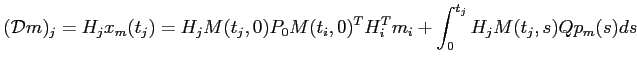
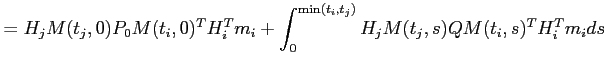
car pour
ce qui démontre que
Sous l'hypothèse (non restrictive) ![]() et
et ![]() symétriques définies positives,
l'opérateur
symétriques définies positives,
l'opérateur
![]() est alors symétrique non négatif.
est alors symétrique non négatif.
![]() est alors un
opérateur symétrique défini positif puisque
est alors un
opérateur symétrique défini positif puisque ![]() est symétrique défini
positif.
est symétrique défini
positif.
L'existence et l'unicité de ![]() en découle directement. La solution optimale
en découle directement. La solution optimale
![]() du problème primal et la variable adjointe
du problème primal et la variable adjointe ![]() vérifient le système d'optimalité (5.25). On peut
donc décomposer
vérifient le système d'optimalité (5.25). On peut
donc décomposer ![]() sous la forme
sous la forme
![]() ,
avec
,
avec
![]() la solution de
la solution de
Enfin, par définition,
ce qui achève la démonstration.
Pour résoudre l'équation (5.29), étant donné que
![]() est symétrique défini positif, une méthode de gradient
permet d'approcher assez rapidement la solution. Il faut donc
définir la fonctionnalle quadratique associée, appelée
fonctionnelle duale :
est symétrique défini positif, une méthode de gradient
permet d'approcher assez rapidement la solution. Il faut donc
définir la fonctionnalle quadratique associée, appelée
fonctionnelle duale :