Figure 6.14: Résultat de la minimisation de la fonction coût primale en utilisant observations. Couche de surface de la solution au début (a) et à la fin (b) de la période d'assimilation.

(a)   (b)

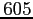
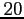
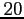
La figure 6.14 montre la couche de surface de l'état initial reconstitué et l'état final correspondant de la période d'assimilation, obtenus avec la méthode primale en utilisant observations, c'est-à-dire une tous les pas d'espace, tous les pas de temps.

Figure 6.15: Résultat de la minimisation de la fonction coût primale en utilisant observations. Couche de surface de la solution au début (a) et à la fin (b) de la période d'assimilation.

(a)   (b)

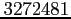
Les résultats équivalents à la figure précédente sont représentés sur la figure 6.15 lorsqu'on utilise observations (tous les pas d'espace sur la grille de surface et à tous les pas de temps).

On constate que la reconstitution de l'état initial est bien meilleure lorsque beaucoup d'observations sont utilisées, même si les champs obtenus ne sont pas tout à fait lisses. En effet, à tout instant, on souhaite que la trajectoire identifiée soit proche des observations bruitées (dont les champs sont représentés sur la figure 6.3), ce qui laisse peu de place au modèle pour essayer de lisser les champs. Par contre, lorsque peu d'observations sont utilisées, la reconstruction de l'état initial est partielle, mais celui-ci est plus régulier puisque le point de départ de la minimisation est un champ lisse (l'état réel du système mais à un instant différent) et peu de contraintes bruitées agissent sur l'évolution de l'état identifié au cours de la minimisation de la fonction coût.

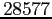
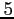
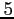
La figure 6.6, qui montrait les mêmes résultats en utilisant observations, est une sorte de moyenne entre les deux précédentes figures. En effet, avec des observations tous les pas d'espace, tous les pas de temps, on obtenait une meilleure reconstitution mais un champ moins lisse que lorsque peu d'observations sont utilisées, et une moins bonne reconstitution mais plus lisse qu'avec beaucoup d'observations.