Conclusions et remarques sur les deux
méthodes numériques

Nous avons tout d'abord testé la convergence numérique de l'algorithme dual et nous avons constaté que la fonctionnelle duale était relativement bien diminuée au cours des premières dizaines d'itérations dans l'algorithme de minimisation. Nous avons ensuite cherché à estimer la part d'erreur numérique et la part de non équivalence mathématique entre les deux méthodes sur un problème de plus petite dimension, en les testant tout d'abord sur une version strictement linéaire du modèle, puis sur le modèle non linéaire. Nous avons constaté que la méthode duale fournissait de meilleurs résultats sur le modèle non linéaire, bien qu'un peu moins bonne sur le modèle linéarisé.

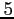
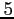
Nous avons ensuite comparé les deux approches dans plusieurs cas de figure. Tout d'abord dans un cadre standard, sans erreur modèle et avec des observations disponibles en quantité relative (tous les points de grille en surface, tous les pas de temps). Nous avons alors constaté que les deux méthodes sont relativement équivalentes, avec un léger avantage numérique pour l'approche duale puisque celle-ci donne de légèrement meilleurs résultats, globalement sur toute la période d'assimilation, que la méthode primale. Néanmoins, les lignes de niveau sont nettement moins lisses, et des prévisions à long terme (si elles pouvaient s'avérer fiables) seraient complètement perturbées par ces irrégularités qui croissent avec le temps.

Lorsque nous rajoutons un terme d'erreur dans le modèle pour simuler toutes les imperfections du modèle (paramètres mal estimés, simplifications inadaptées, ...), la méthode primale montre clairement ses limites alors que la méthode duale est relativement moins perturbée par la présence de ce terme d'erreur. Par contre, la méthode primale conserve des lignes de niveau assez lisses, contrairement aux solutions duales qui ont toujours beaucoup d'irrégularités, qui pourraient s'avérer gênantes pour des prévisions à long terme. Nous avons également constaté la tendance chaotique du modèle puisqu'il a été impossible de mettre un terme d'erreur trop important, sous peine de voir une bonne partie des intégrations directes du modèle exploser numériquement.

Nous avons ensuite testé la sensibilité des deux méthodes à la quantité d'observations disponibles pour l'assimilation. Lorsque le nombre d'observations disponibles est trop faible, les deux méthodes souffrent d'un manque d'information. Lorsque ce nombre est trop élevé au contraire, les minimisations s'avèrent plus délicates et ont tendance à ralentir ou détériorer les reconstitutions de l'état initial. La méthode duale s'avère plus performante lorsque le nombre d'observations est plus petit que la dimension d'un vecteur d'état, puisque elle travaille sur un espace de dimension plus petite que l'algorithme primal, mais lorsqu'on dispose de plus d'observations que de points dans la grille de discrétisation, la méthode duale est pénalisée en travaillant sur un espace trop grand.

Enfin, nous avons constaté que la méthode duale était capable, dans une certaine mesure, de mieux identifier la condition initiale à partir d'observations issues d'un modèle bruité, mais aussi de mieux faire évoluer la trajectoire dans le temps en intégrant un terme correctif dans le modèle et donc de mieux simuler le modèle bruité. La méthode primale n'a pu, quant à elle, que chercher une trajectoire pour le modèle non bruité, et a donc conduit à une identification moins performante.