Les observations sont réalisées à intervalles de temps réguliers, à des endroits fixés choisis aléatoirement. Les observations sont alors bruitées. Les erreurs d'observation suivent une loi normale, sont décorrélées et ont toutes la même variance, proportionnelle à la matrice identité.
Le maillage à grande résolution utilisé pour discrétiser
le domaine comporte ![]() points de grille, et la
dimension du problème discrétisé est donc
points de grille, et la
dimension du problème discrétisé est donc ![]() .
Mais dans un premier temps, nous utiliserons une grille de
discrétisation à faible résolution, avec seulement
.
Mais dans un premier temps, nous utiliserons une grille de
discrétisation à faible résolution, avec seulement
![]() points, et donc la dimension du
vecteur de contrôle est restreinte à
points, et donc la dimension du
vecteur de contrôle est restreinte à ![]() afin de pouvoir effectuer
un grand nombre d'itérations. Le nombre de paires
afin de pouvoir effectuer
un grand nombre d'itérations. Le nombre de paires ![]() stockées
est
stockées
est ![]() . Les paramètres de recherche linéaire de Wolfe sont
. Les paramètres de recherche linéaire de Wolfe sont
![]() et
et ![]() . Le nombre maximal d'itérations a
été fixé à
. Le nombre maximal d'itérations a
été fixé à ![]() , et le nombre maximal d'évaluations de la
fonction coût et de son gradient est
, et le nombre maximal d'évaluations de la
fonction coût et de son gradient est ![]() (le nombre maximal
d'itérations augmenté d'un cinquième de sa valeur). La
décroissance attendue de la fonction coût à la première
itération est la moitié de sa valeur. La fonctionnelle quadratique
approchée que l'on souhaite minimiser est la suivante :
(le nombre maximal
d'itérations augmenté d'un cinquième de sa valeur). La
décroissance attendue de la fonction coût à la première
itération est la moitié de sa valeur. La fonctionnelle quadratique
approchée que l'on souhaite minimiser est la suivante :
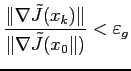
où
La qualité de l'approximation de la hessienne inverse L-BFGS est mesurée en calculant le spectre de
Afin de pouvoir mesurer aussi de manière relative cette qualité, le spectre de
Dans les deux cas, le spectre est calculé en utilisant une méthode de type Arnoldi [26].
Même si nous nous sommes essentiellement intéressés à la qualité de l'approximation de la hessienne L-BFGS, nous avons également regardé l'efficacité de l'algorithme de minimisation en mesurant le nombre d'itérations et de simulations (évaluations de la fonction coût et de son gradient) nécessaires à la convergence.