


suivant: Q.R. d'ordre supérieur en
monter: Variantes sur la quasi-réversibilité
précédent: Variantes sur la quasi-réversibilité
Table des matières
L'équation considérée comme problème rétrograde est désormais la suivante :
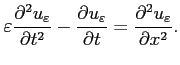 |
(4.8) |
On se réserve désormais le droit de prendre
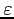 négatif puisqu'il n'est pas évident de savoir quel signe mettre
devant le terme d'ordre
négatif puisqu'il n'est pas évident de savoir quel signe mettre
devant le terme d'ordre 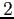 en temps. Si
en temps. Si
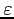 est choisi
positif, l'équation (4.8) est du type équation des ondes,
et il suffit de mettre les conditions aux bords suivantes pour obtenir
l'existence et l'unicité de la solution :
est choisi
positif, l'équation (4.8) est du type équation des ondes,
et il suffit de mettre les conditions aux bords suivantes pour obtenir
l'existence et l'unicité de la solution :
Par contre, si
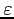 est choisi négatif, l'équation (4.8)
s'apparente à une équation de Laplace et il faudrait se donner une condition initiale,
une condition finale et une condition sur les bords pour avoir un problème bien posé.
Malheureusement, il est impossible de se donner numériquement une condition
finale puisque c'est ce que l'on cherche à identifier. Nous allons donc imposer
les mêmes conditions aux bords que pour
est choisi négatif, l'équation (4.8)
s'apparente à une équation de Laplace et il faudrait se donner une condition initiale,
une condition finale et une condition sur les bords pour avoir un problème bien posé.
Malheureusement, il est impossible de se donner numériquement une condition
finale puisque c'est ce que l'on cherche à identifier. Nous allons donc imposer
les mêmes conditions aux bords que pour
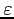 positif dans un cadre strictement
numérique.
positif dans un cadre strictement
numérique.
Figure 4.5:
Solutions optimales du problème (4.8)
pour des valeurs de
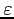 respectivement positives (a) et
négatives (b).
respectivement positives (a) et
négatives (b).
![\includegraphics[width=6cm]{chap5.fig/new_1_5.eps}](img349.png) |
|
![\includegraphics[width=6cm]{chap5.fig/2_neg.eps}](img350.png) |
| (a) |
|
(b) |
|
Les figures 4.5-a et -b montrent les solutions optimales de
ce dernier problème (puis, pour les temps positifs, les solutions de
l'équation de la chaleur directe) pour des valeurs de
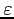 choisies respectivement positives et négatives. L'intervalle de
temps sur lequel ont été intégrées les solutions est de
nouveau de longueur
choisies respectivement positives et négatives. L'intervalle de
temps sur lequel ont été intégrées les solutions est de
nouveau de longueur 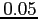 , car comme précédemment, lorsque
celui-ci est choisi trop grand (
, car comme précédemment, lorsque
celui-ci est choisi trop grand (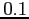 ou plus), les résultats
empirent assez vite.
ou plus), les résultats
empirent assez vite.
Dans un cas comme dans l'autre, la solution construite est très
mauvaise, avec une erreur relative de plus de 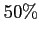 . Par contre, on
peut noter une différence de courbure entre la figure
4.5-a et toutes les autres figures obtenues dans ce
chapitre. Ceci intervient lorsque le paramètre
. Par contre, on
peut noter une différence de courbure entre la figure
4.5-a et toutes les autres figures obtenues dans ce
chapitre. Ceci intervient lorsque le paramètre
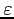 est
choisi parmi les réels strictement négatifs, et donc pour un
problème de nature elliptique.
est
choisi parmi les réels strictement négatifs, et donc pour un
problème de nature elliptique.
Cette méthode apparaissant comme nettement moins bonne que la
méthode Q.R. originale, nous ne nous sommes pas attardés à faire
de plus amples tests numériques.



suivant: Q.R. d'ordre supérieur en
monter: Variantes sur la quasi-réversibilité
précédent: Variantes sur la quasi-réversibilité
Table des matières
Retour à la page principale
![\begin{displaymath}\begin{array}{ll}
\displaystyle u_\varepsilon (x,0)=\chi(x), ...
...(x,t)=0, \quad & x \in \partial \Omega, t\in]0,T[.
\end{array}\end{displaymath}](img348.png)
![]() choisies respectivement positives et négatives. L'intervalle de
temps sur lequel ont été intégrées les solutions est de
nouveau de longueur
choisies respectivement positives et négatives. L'intervalle de
temps sur lequel ont été intégrées les solutions est de
nouveau de longueur ![]() , car comme précédemment, lorsque
celui-ci est choisi trop grand (
, car comme précédemment, lorsque
celui-ci est choisi trop grand (![]() ou plus), les résultats
empirent assez vite.
ou plus), les résultats
empirent assez vite.
![]() . Par contre, on
peut noter une différence de courbure entre la figure
4.5-a et toutes les autres figures obtenues dans ce
chapitre. Ceci intervient lorsque le paramètre
. Par contre, on
peut noter une différence de courbure entre la figure
4.5-a et toutes les autres figures obtenues dans ce
chapitre. Ceci intervient lorsque le paramètre
![]() est
choisi parmi les réels strictement négatifs, et donc pour un
problème de nature elliptique.
est
choisi parmi les réels strictement négatifs, et donc pour un
problème de nature elliptique.