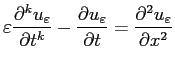 |
(4.9) |
L'équation que nous allons utiliser pour remonter le temps est maintenant la suivante :
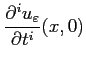 pour
pour
Les solutions de cette équation sont représentées sur la
figure 4.6, pour des valeurs de ![]() choisies égales
à
choisies égales
à ![]() (a) et
(a) et ![]() (b) respectivement. Pour
(b) respectivement. Pour ![]() , la méthode ne
donne absolument rien. En effet, on assiste à un changement de signe
de la solution, puis à une tendance à diverger fortement. En
partant après d'une telle condition initiale pour le problème de
la chaleur classique, non seulement la solution obtenue est trop
grande en norme, mais elle est de signe opposé à ce à quoi on
s'attend.
, la méthode ne
donne absolument rien. En effet, on assiste à un changement de signe
de la solution, puis à une tendance à diverger fortement. En
partant après d'une telle condition initiale pour le problème de
la chaleur classique, non seulement la solution obtenue est trop
grande en norme, mais elle est de signe opposé à ce à quoi on
s'attend.
Par contre, lorsqu'on choisit ![]() égal à
égal à ![]() , on retrouve une
solution qui a la même allure générale qu'avec la méthode
Q.R. classique. L'erreur minimale (mesurée en norme infinie entre
, on retrouve une
solution qui a la même allure générale qu'avec la méthode
Q.R. classique. L'erreur minimale (mesurée en norme infinie entre
![]() et la condition finale reconstruite) est d'environ
et la condition finale reconstruite) est d'environ ![]() , et
donc bien supérieure à celle obtenue avec la méthode
originale. De plus, ce minimum est atteint pour une valeur de
, et
donc bien supérieure à celle obtenue avec la méthode
originale. De plus, ce minimum est atteint pour une valeur de
![]() égale à
égale à ![]() . Cette valeur est bien trop importante
pour ne pas dénaturer l'équation de la chaleur.
. Cette valeur est bien trop importante
pour ne pas dénaturer l'équation de la chaleur.
D'autres tests ont été réalisés dans ce dernier cas (![]() )
mais aucun n'a permis d'obtenir des résultats plus concluants.
)
mais aucun n'a permis d'obtenir des résultats plus concluants.
Il apparaît donc que la méthode Q.R. originale, bien que peu satisfaisante, reste la meilleure méthode testée ici avec l'équation de la chaleur. L'équation de la chaleur constitue le premier modèle sur lequel nous avons testé la quasi-réversibilité puisque c'est une équation d'évolution relativement simple, et dont l'instabilité rétrograde est fort bien connue. Néanmoins, cette équation est trop éloignée des systèmes habituellement utilisés en océanographie car, notamment, elle est linéaire. Il convient donc d'essayer la quasi-réversibilité sur un système différentiel non linéaire, à comportement chaotique.