


suivant: Remarques sur la méthode
monter: Nudging direct
précédent: Principe de la méthode
Table des matières
Nous allons vérifier sur un exemple linéaire que le terme de rappel
introduit dans l'équation conduit bien à stabiliser la solution
autour des observations. Considérons un problème simplifié
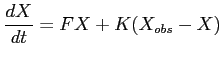 |
(4.16) |
où 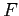 est linéaire et où l'opérateur d'observation
est linéaire et où l'opérateur d'observation 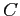 est
égal à l'identité. Notons
est
égal à l'identité. Notons 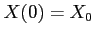 la condition initiale.
Nous supposerons enfin que
la condition initiale.
Nous supposerons enfin que 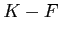 est inversible, afin de
simplifier le problème. Alors la solution du problème est
est inversible, afin de
simplifier le problème. Alors la solution du problème est
et il est clair que si on fait tendre 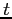 vers
vers 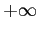 et que la
matrice
et que la
matrice 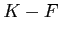 est positive,
la solution
est positive,
la solution 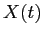 tendra vers la solution du problème stationnaire
tendra vers la solution du problème stationnaire
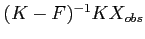 .
Si on choisit la matrice
.
Si on choisit la matrice
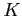 suffisamment grande (i.e. avec des valeurs propres suffisamment
grandes), on assure la positivité de
suffisamment grande (i.e. avec des valeurs propres suffisamment
grandes), on assure la positivité de 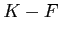 et, de plus, la solution sera
alors proche de
et, de plus, la solution sera
alors proche de 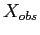 au voisinage de
au voisinage de 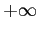 .
.
On remarquera également que si on choisit la matrice 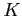 trop petite
(de sorte que toutes les valeurs propres de la matrice
trop petite
(de sorte que toutes les valeurs propres de la matrice 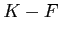 soient négatives),
alors la solution s'éloigne exponentiellement en temps de
soient négatives),
alors la solution s'éloigne exponentiellement en temps de 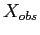 .
.



suivant: Remarques sur la méthode
monter: Nudging direct
précédent: Principe de la méthode
Table des matières
Retour à la page principale
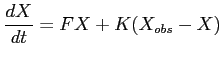
![]() trop petite
(de sorte que toutes les valeurs propres de la matrice
trop petite
(de sorte que toutes les valeurs propres de la matrice ![]() soient négatives),
alors la solution s'éloigne exponentiellement en temps de
soient négatives),
alors la solution s'éloigne exponentiellement en temps de ![]() .
.