L'écriture du problème sous la forme (4.16) permet de faire apparaître
un lien assez clair avec les méthodes séquentielles reposant sur le filtre de Kalman.
En effet, si la matrice de nudging ![]() est convenablement choisie, le nudging ainsi utilisé
se ramène à un filtrage de Kalman, et en conséquence, pour un problème linéaire,
le nudging optimal est équivalent au filtre de Kalman.
est convenablement choisie, le nudging ainsi utilisé
se ramène à un filtrage de Kalman, et en conséquence, pour un problème linéaire,
le nudging optimal est équivalent au filtre de Kalman.
En prenant l'opérateur d'observation ![]() égal à l'identité et en écrivant un
schéma temporel aux différences finies pour (4.16), on peut écrire
le problème sous la forme
égal à l'identité et en écrivant un
schéma temporel aux différences finies pour (4.16), on peut écrire
le problème sous la forme
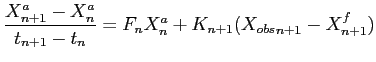
où
En résolvant d'abord l'équation (4.14) du temps ![]() au temps
au temps ![]() en partant
de
en partant
de ![]() pour construire l'ébauche
pour construire l'ébauche ![]() , on retrouve la formule (2.9)
du filtre de Kalman. En remplaçant
, on retrouve la formule (2.9)
du filtre de Kalman. En remplaçant ![]() par
par
![]() , la formule
donnant
, la formule
donnant ![]() est alors exactement l'équation (2.11) donnant le nouvel
état analysé dans la méthode du filtre de Kalman. L'équivalence des deux méthodes est
alors vérifiée en choisissant à chaque instant comme matrice de nudging la matrice de gain
du filtre de Kalman.
est alors exactement l'équation (2.11) donnant le nouvel
état analysé dans la méthode du filtre de Kalman. L'équivalence des deux méthodes est
alors vérifiée en choisissant à chaque instant comme matrice de nudging la matrice de gain
du filtre de Kalman.