Le système de Lorenz est un jeu de trois équations différentielles
non linéaires couplées faisant intervenir les trois variables
![]() :
:
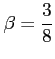 .
.
|
La figure 4.7-a montre l'évolution du vecteur
![]() sur l'intervalle de temps
sur l'intervalle de temps ![]() ,
obtenue en intégrant le système de Lorenz à partir de la
condition initiale
,
obtenue en intégrant le système de Lorenz à partir de la
condition initiale
![]() au temps
au temps ![]() . La figure
4.7-b correspond à l'évolution de la variable
. La figure
4.7-b correspond à l'évolution de la variable
![]() en fonction du temps à partir des mêmes conditions
initiales. Les deux régimes du système de Lorenz correspondent à
des oscillations autour de deux points fixes instables du système,
symétriques par rapport à l'axe
en fonction du temps à partir des mêmes conditions
initiales. Les deux régimes du système de Lorenz correspondent à
des oscillations autour de deux points fixes instables du système,
symétriques par rapport à l'axe ![]() . Les oscillations
autour de chacun des points fixes, pendant lesquelles la variable
. Les oscillations
autour de chacun des points fixes, pendant lesquelles la variable ![]() garde un signe constant, sont clairement visibles sur la figure
4.7, et ont une période de l'ordre de
garde un signe constant, sont clairement visibles sur la figure
4.7, et ont une période de l'ordre de ![]() . Leur
amplitude augmente progressivement, et après quelques oscillations,
une transition a lieu vers l'autre point fixe. Les transitions
correspondent à un changement de signe de
. Leur
amplitude augmente progressivement, et après quelques oscillations,
une transition a lieu vers l'autre point fixe. Les transitions
correspondent à un changement de signe de ![]() .
.
En notant ![]() le vecteur position et
le vecteur position et
![]() ;
;
![]() ;
;
![]() le vecteur
vitesse, le système de Lorenz s'écrit exactement sous la forme de
l'équation (4.14).
le vecteur
vitesse, le système de Lorenz s'écrit exactement sous la forme de
l'équation (4.14).