![$\displaystyle \left\{ \begin{array}{l} \displaystyle \frac{dx}{dt} = \sigma (y-...
... xz, [0.4cm] \displaystyle \frac{dz}{dt} = \beta z + xy, \end{array} \right.$](img362.png) |
(4.10) |
Des tests ont tout d'abord été réalisés sur le système de Lorenz, un système non linéaire chaotique relativement simple. Nous présentons rapidement les équations du système de Lorenz (il sera étudié plus en détail dans la suite de ce chapitre) :
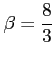 .
En notant
.
En notant
Directement, cela est numériquement impossible. En effet, la solution
diverge avant le temps ![]() alors que les trajectoires du système
direct n'auraient pas oscillé plus d'une fois dans le même temps.
alors que les trajectoires du système
direct n'auraient pas oscillé plus d'une fois dans le même temps.
Les équations Q.R. considérées sont les suivantes :
Malheureusement, aucune de ces deux équations n'a donné de
résultats numériques intéressants : la trajectoire diverge
toujours aussi rapidement, et il n'est pas envisageable de travailler
sur des intervalles de longueur inférieure à la période moyenne
(de l'ordre de ![]() ) des oscillations des trajectoires directes. Les
autres variantes de la méthode Q.R. présentées précédemment
ont également été testées sur le système de Lorenz, toujours
sans succès.
) des oscillations des trajectoires directes. Les
autres variantes de la méthode Q.R. présentées précédemment
ont également été testées sur le système de Lorenz, toujours
sans succès.
Des tests sommaires ont également été réalisés sur un modèle océanique quasi-géostrophique barotrope, toujours sans succès.